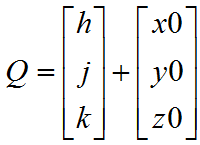El método
de Newton Raspón Multivariable es utilizado principalmente para resolver
sistemas de ecuaciones lineales y no lineales, este método posee la característica
de poder conseguir la solución de dos o más variables dentro de un determinado
sistema de ecuaciones, siempre respetando la condición de la igualdad del
numero de incógnitas y el numero de ecuaciones necesarias para dar solución a
un determinado problema.
Considerando
que se tiene un sistema de 3 ecuaciones
Y partiendo
de la serie de Taylor como base principal para el uso del método
Para que el método llegue a un criterio de
convergencia se asume que la evaluación de las funciones son iguales a cero.
Reemplazando
la condición asumida anteriormente en el sistema encontrado por la serie de
Taylor, se encuentra el siguiente sistema de ecuaciones.
Donde:
Substituyendo
h, j y k en el sistema de ecuaciones
Para hallar los valores de h, j y k del sistema de ecuaciones anterior
Se asume que
y
Para hallar h, j y k se calcula el inverso de la matriz A multiplicado por la matriz B segundo la siguiente formula.
P=inv(A)*B
el resultado del calculo anterior es igual a:
para hallar los nuevos valores de x1, y1 y z1
se asume que
y el valor de x1, y1 y z1 se encuentra cuando
El criterio de convergencia se cumple cuando se evalua los nuevos valores de x1, y1 y z1 en las funciones f1, f2, y f3 para encontrar a convergencia del resultado
A continuación
se presenta el diagrama de flujo del método
A continuación
el código del método desarrollado para MATLAB
function Sistema;
clc
clear
disp('=======================ANDY===========AVIMAEL===================');
disp('======Método
de Newton Raphson Para Un Sistema de 3x3===========');
disp('======================SAAVEDRA=======MENDOZA====================');
f1=input('Ingrese la
funcion 1 f (x,y,z)=0....');
f2=input('Ingrese la
funcion 2 f (x,y,z)=0....');
f3=input('Ingrese la
funcion 3 f (x,y,z)=0....');
x0=input('ingrese el
valor inicial de x=');
y0=input('ingrese el
valor inicial de y=');
z0=input('ingrese el
valor inicial de z=');
l=0.00001;
tol=input('Ingrese la
tolerancia=');
disp('===============a=========n===========d==============y============================');
disp(' N X0 Y0 Z0 T0 error');
cont=0;
disp('===s====a====a=====v=======e========d========r===========a========================');
while 1
cont=cont+1;
a1=(f1(x0+l,y0,z0)-f1(x0,y0,z0))/(l);
d1=(f2(x0+l,y0,z0)-f2(x0,y0,z0))/(l);
g1=(f3(x0+l,y0,z0)-f3(x0,y0,z0))/(l);
b1=(f1(x0,y0+l,z0)-f1(x0,y0,z0))/(l);
e1=(f2(x0,y0+l,z0)-f2(x0,y0,z0))/(l);
h1=(f3(x0,y0+l,z0)-f3(x0,y0,z0))/(l);
c1=(f1(x0,y0,z0+l)-f1(x0,y0,z0))/(l);
f11=(f2(x0,y0,z0+l)-f2(x0,y0,z0))/(l);
i1=(f3(x0,y0,z0+l)-f3(x0,y0,z0))/(l);
j1=[a1 b1 c1 ;d1 e1 f11 ;g1 h1 i1];
Fz=[f1(x0,y0,z0); f2(x0,y0,z0);
f3(x0,y0,z0)];
Q=(inv(j1))*(-Fz);
X11=[x0; y0; z0];
P=X11+Q;
x0=P(1);
y0=P(2);
z0=P(3);
er=sum(abs(Fz));
fprintf('%12.0f %12.8f
%12.8f %12.8f %12.8f \n',cont,x0,y0,z0,er);
if er<tol;
disp('los valores de x,y,z son;');
disp('El valor de x es= ');
fprintf(' %12.8f\n',x0);
disp('El valor de y es= ');
fprintf(' %12.8f\n',y0);
disp('El valor de z es= ');
fprintf(' %12.8f\n',z0);
disp('Con un error de;');
fprintf('%12.8f\n',er);
break
end
end
disp('=================================================================');
end
El codigo del método se encuentra en el siguiente link
A continuación se muestra un ejemplo y la prueba del programa